Masking#
The template mask is pivotal for the normalization of the cross-correlation coefficient. The composition of an optimal mask is problem-specific, but we recommend the following when designing masks
The mask should focus on conserved key features.
Consider the context in which the mask will be applied. Particularly for in situ images, crowdedness can be problematic if the mask is excessively large.
Sharp transitions or edge effects should be avoided by smoothing or sufficiently sized boxes.
Next to template masks pytme also supports masks for the target, the integration of which depends on the used score. Typically however, target masks are used to remove regions rich in contaminants.
Mask Design#
While filtering typically has greater impact on the performance than the choice of mask, chosing a suitable mask still helps to improve performance.
By default, pytme uses the entire area under the template as mask. However, this results in wide peaks, which is disadvantageous in corwded settings. When focusing on more defining features using an ellipsoidal mask we observe a sharpening of the peak and a decrease in background score. However, if we make the mask too narrow, as illustrated by the last example, the mask no longer provides a faithful approximation of the cross-correlation background and as thus the template matching scores become uninformative.
(Source code, png, hires.png, pdf)

Influence of mask design on template matching scores.#
Mask Smoothing#
The masks showed in the previous section contained sharp edges, which are troublesome to represent in Fourier space. In the following we look at the effect of smoothing the ellipsoidal mask using a Gaussian filter.
Albeit difficult to see in this representation, smoothing the mask with a sigma of two results in 5% higher peaks, compared to their individual backgrounds. Nevertheless, the benefit of smoothing masks is less obvious and has to be evaluated on a per-problem basis.
(Source code, png, hires.png, pdf)
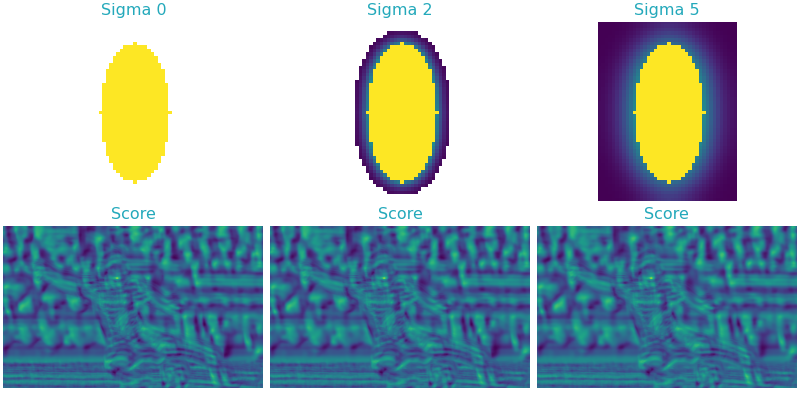
Influence of mask smoothing on template matching scores.#
Note
The choice of mask also has an impact on the runtime performance of template matching. Rotation symmetric masks require less Fourier tarnsforms, thus reducing runtime by up to a factor of three.
A more complete treatment of the mathematical implications of using different masks is provided in [1], together with explanatory slides. Alternatively, this OpenCV tutorial provides further examples on the effect of masking.